設(shè)隨機(jī)變量X~N(1,4),則P(-1<X<3)等于多少？

方法一:常規(guī)計(jì)算法

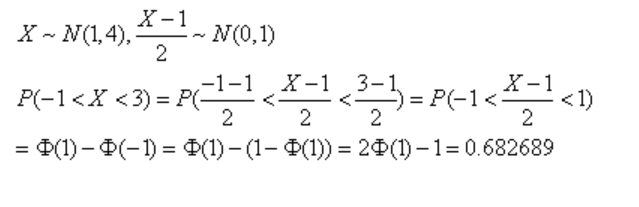
方法二: 推算法

根據(jù)正態(tài)分布經(jīng)驗(yàn)法則,對(duì)于正態(tài)分布X, X在均值加減1倍標(biāo)準(zhǔn)差的范圍變化,X的取值可以覆蓋68.26%的數(shù)據(jù)

本題剛好是這個(gè)特殊情況均值1加減1倍標(biāo)準(zhǔn)差2 (1-2) < X <(1+2 ) --> -1< X<3

所以答案是68.26%,即本題的P(-1< X<3)=0.6826

備注:

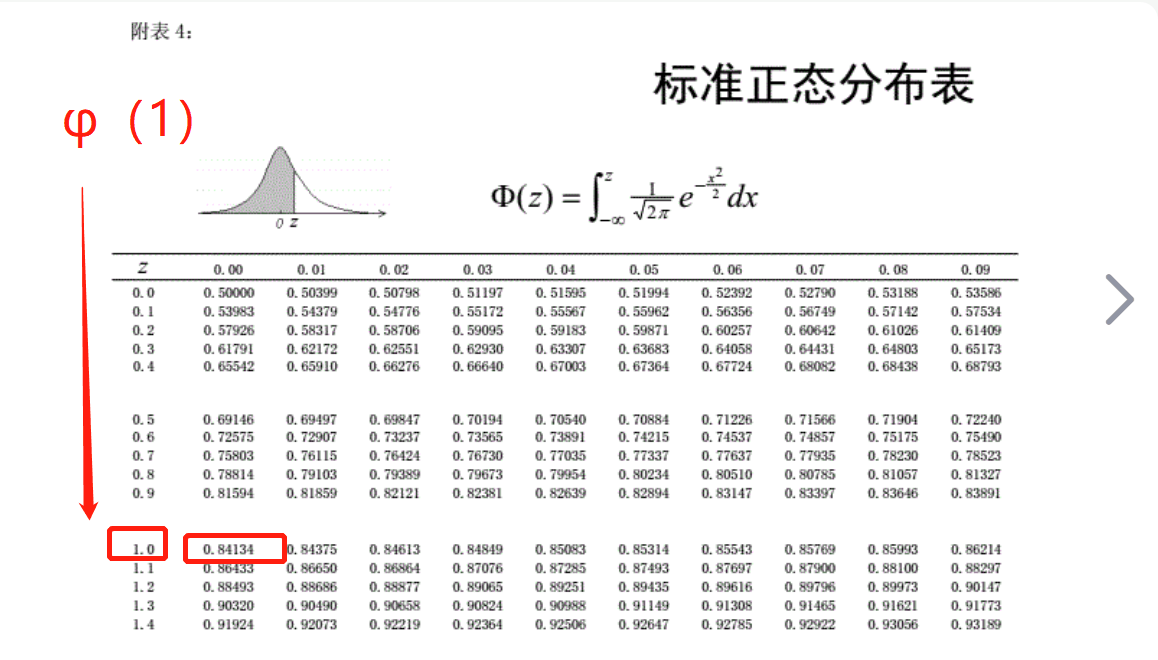
題目中的φ(1)的數(shù)值是查標(biāo)準(zhǔn)正態(tài)分布函數(shù)表得出的,φ(1)作為常用數(shù)值可以記住,有時(shí)候考試不給提示參考φ值

61.6073

關(guān)注作者

評(píng)論(2)

發(fā)表評(píng)論

CDA128449

2022-08-25

標(biāo)準(zhǔn)化處理后，就是一個(gè)（-1，1）之間的正態(tài)分布面積

0.0000 0 0 回復(fù)

sevensky0331

2022-06-22

0.6827，可以把問(wèn)題標(biāo)準(zhǔn)化，化為0，1的標(biāo)準(zhǔn)正態(tài)分布進(jìn)行計(jì)算

0.0000 0 0 回復(fù)

CDA考試動(dòng)態(tài)

CDA報(bào)考指南

推薦帖子

99999久久久久久亚洲,欧美人与禽猛交狂配,高清日韩av在线影院,一个人在线高清免费观看,啦啦啦在线视频免费观看www